Grundlagen der Tourenoptimierung: Die Herausforderung die optimale Route zu finden

Tourenplanung ist ein wichtiger Teil der Einsatzplanung von Servicetechnikern, die ein größeres Gebiet abdecken. Durch eine möglichst optimale Reiseroute und Reihenfolge der Termine lässt sich viel Zeit und somit auch Geld sparen. Doch je mehr Einsätze pro Tag einzuplanen sind und je mehr Techniker ein Disponent in seinem Team hat, desto komplexer wird die Erstellung einer effizienten Route.

Das, was landläufig als optimale Tourenplanung oder Tourenoptimierung bezeichnet wird, ist in der Mathematik bzw. Informatik als Vehicle Routing Problem (VRP) bekannt. Das Problem der Mitarbeitereinsatzplanung in der Praxis ist jedoch kein VRP sondern ein MDVRP, bzw. ein MDVRPTW, aber dazu später mehr.
Eine etwas bekanntere Ableitung ist als “Problem des Handlungsreisenden” bekannt. Die Aufgabe besteht darin, eine Reihenfolge für den Besuch mehrerer Orte so zu wählen, dass

keine Station außer der Ersten mehr als einmal besucht wird
die erste Station gleich der letzten Station ist
die gesamte Reisestrecke möglichst kurz ist

Acht Städte – 40.320 mögliche Routen

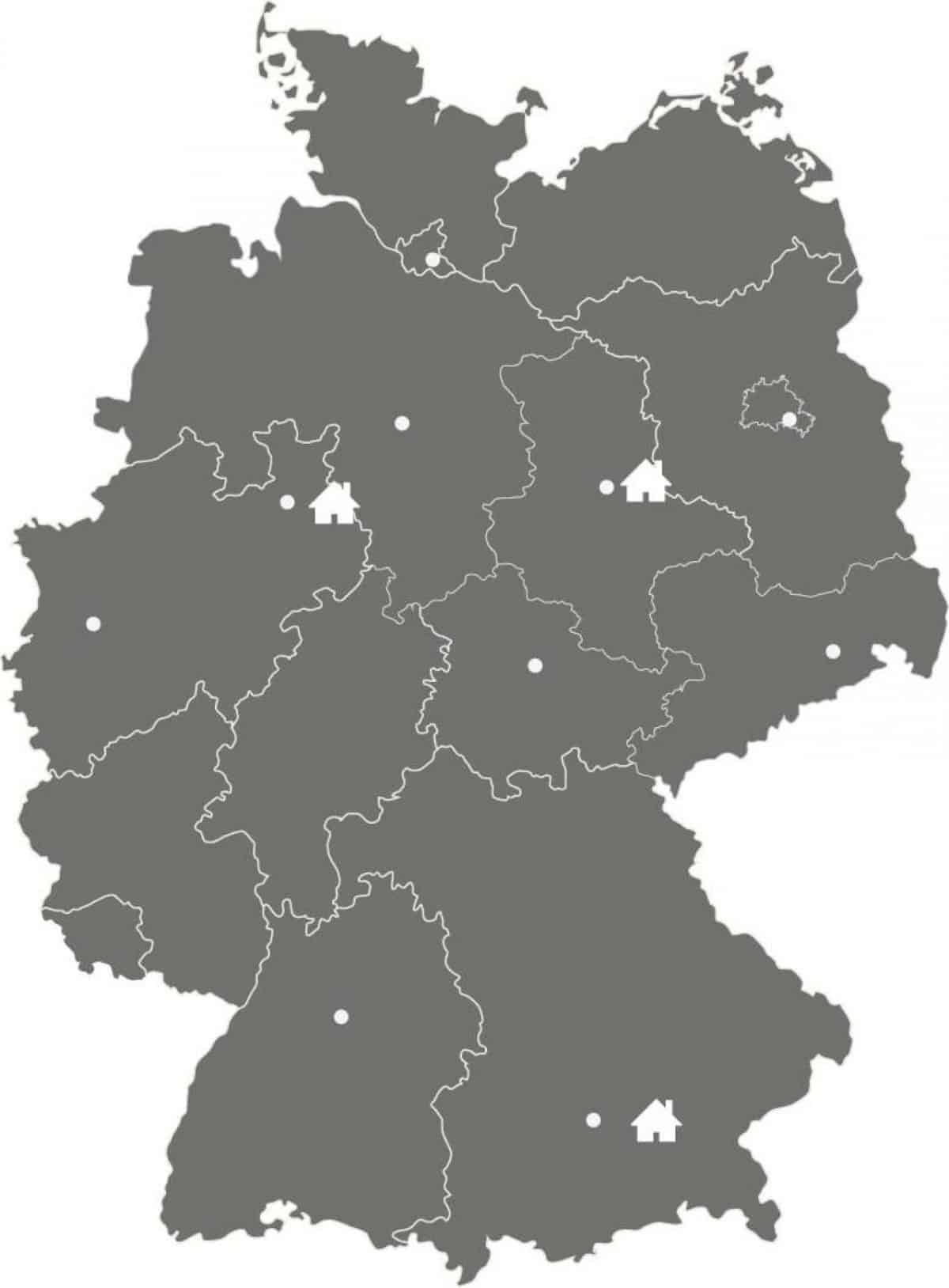
Am Beispiel einer Reise durch acht Städte in Deutschland lässt sich das Problem veranschaulichen. Ausgangs- und Zielort ist München, bereist werden die Städte:

● München (Ausgangs- und Zielort)	● Erfurt
● Berlin	● Hamburg
● Dresden	● Hannover
● Düsseldorf	● Stuttgart

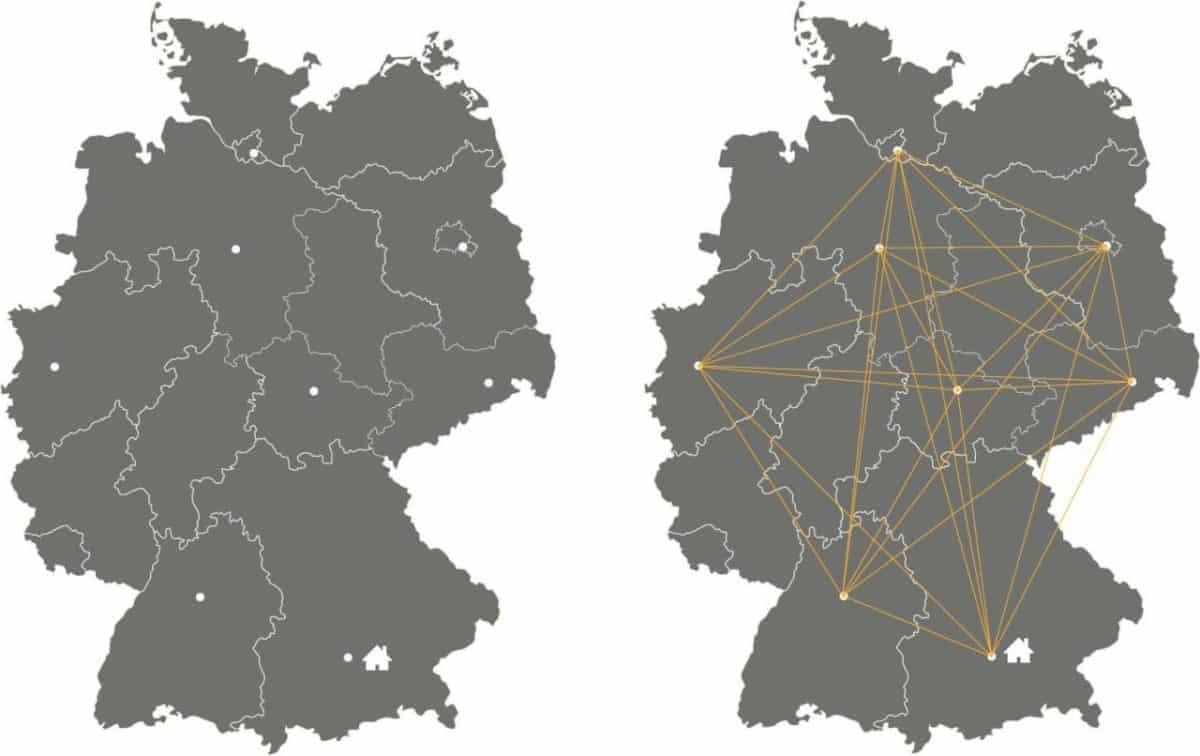
Es gibt über 40.000 verschiedene Möglichkeiten (Reihenfolgen) die sieben Städte zu bereisen – aber welche ist die kürzeste?

Rein mathematisch lässt sich das Problem durch die Fakultät von 8 (als Mathematischer Ausdruck 8!) beschreiben. Das heißt um acht Städte zu bereisen gibt es 40.032 mögliche Reihenfolgen bzw. Touren. Als Tour bezeichnen wir an dieser Stelle eine abgeschlossene Fahrt, die alle Ziele erreicht und wieder zum Ausgangspunkt zurückkehrt.

Planungsvorschlag 1 – Immer zur nächstgelegenen Stadt

Ein relativ einfacher Ansatz zur Lösung ist, von jeder Stadt aus zur unmittelbar nächstliegenden Stadt, die noch nicht besucht wurde, zu reisen.

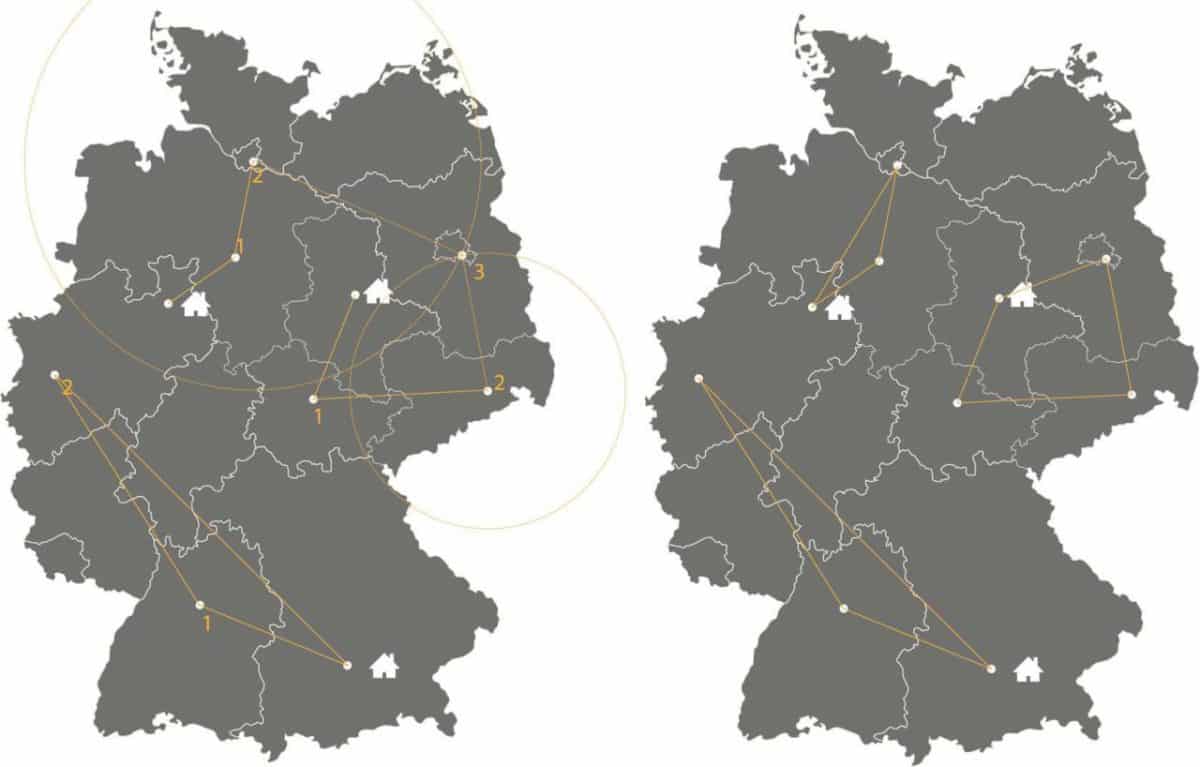
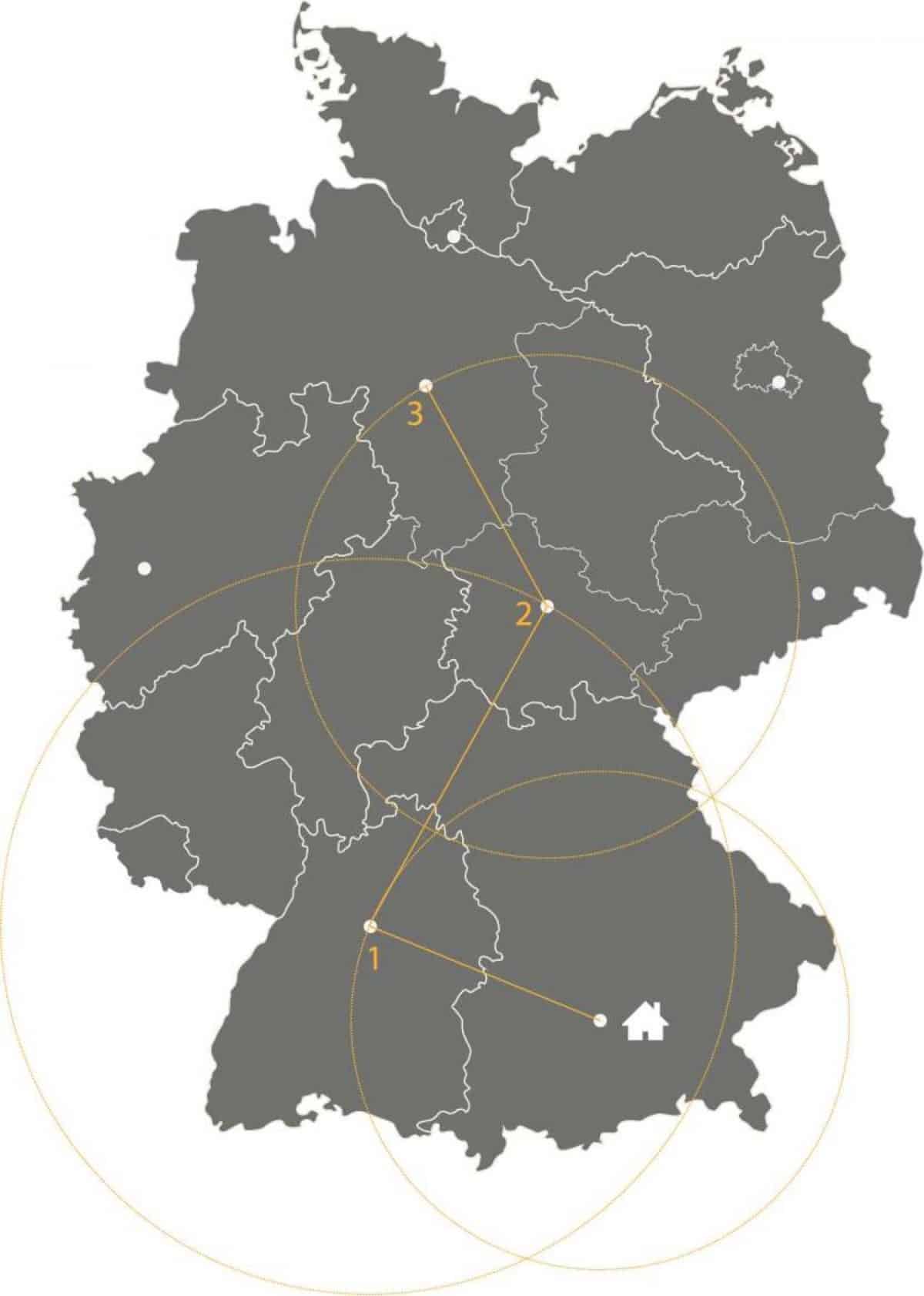Ein einfacher Ansatz zur Berechnung der optimalen Route: Von jedem Ziel zum nächstgelegenen Ziel fahren, das noch nicht besucht wurde.

Im Bild wird dieser Ansatz durch Umkreissuche illustriert, um den jeweils nächsten Zielort zu finden.

Das Ergebnis der Planung – nicht optimal!

Führt man diese Methode fort, erhält man am Ende diese Route:

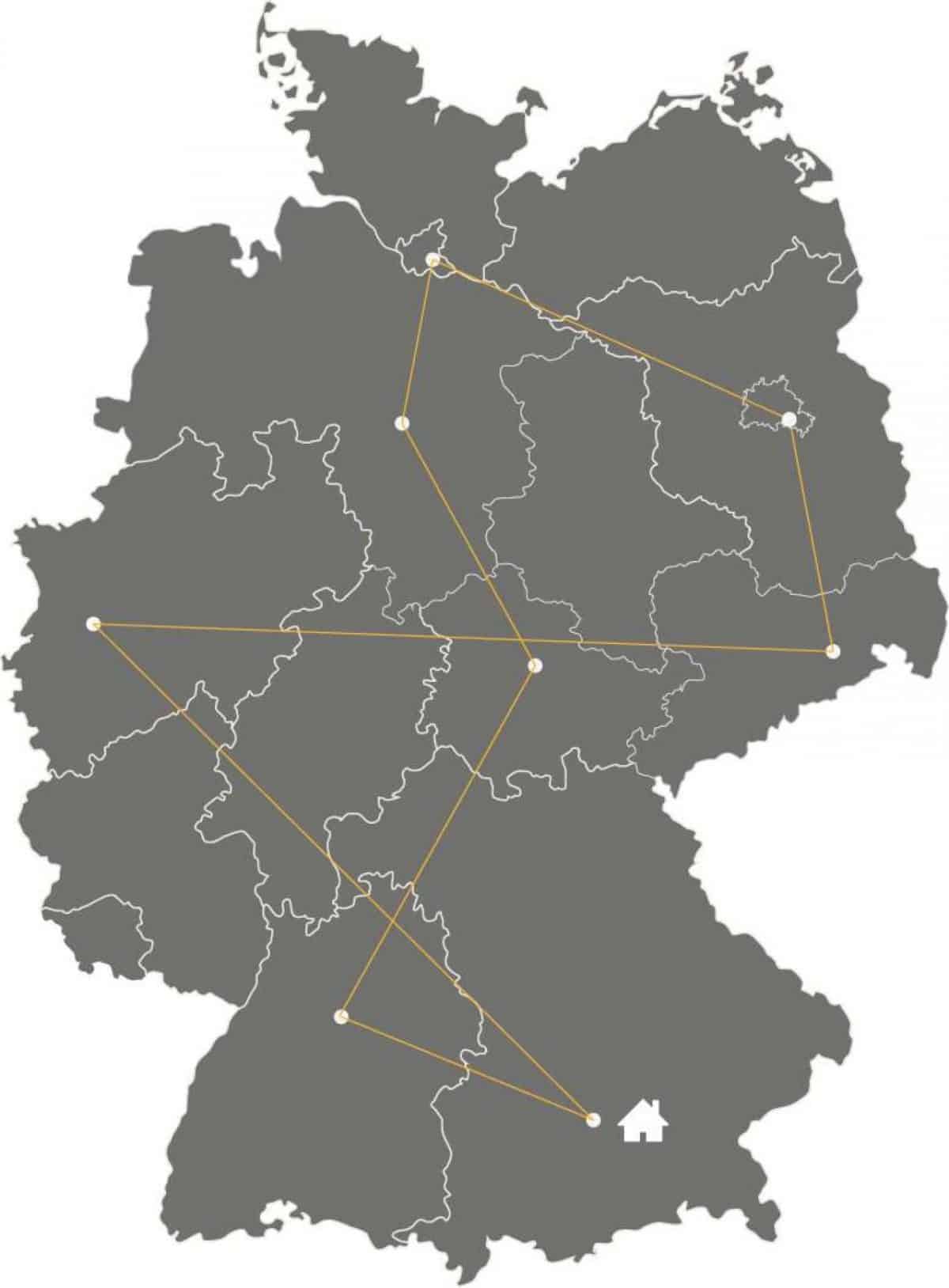Sich kreuzende Routen sind häufig ein Indikator für eine nicht optimale Planung.

Dass dieses Ergebnis nicht optimal ist, sieht man auf den ersten Blick – vor allem anhand der sich überschneidenden Routen. Die für dieses Szenario optimale Route sieht folgendermaßen aus:

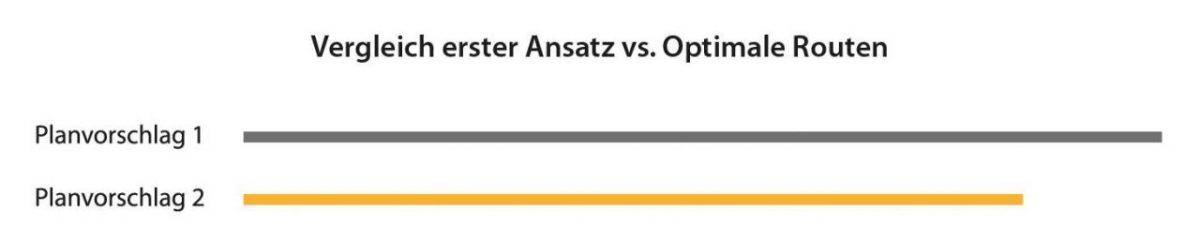
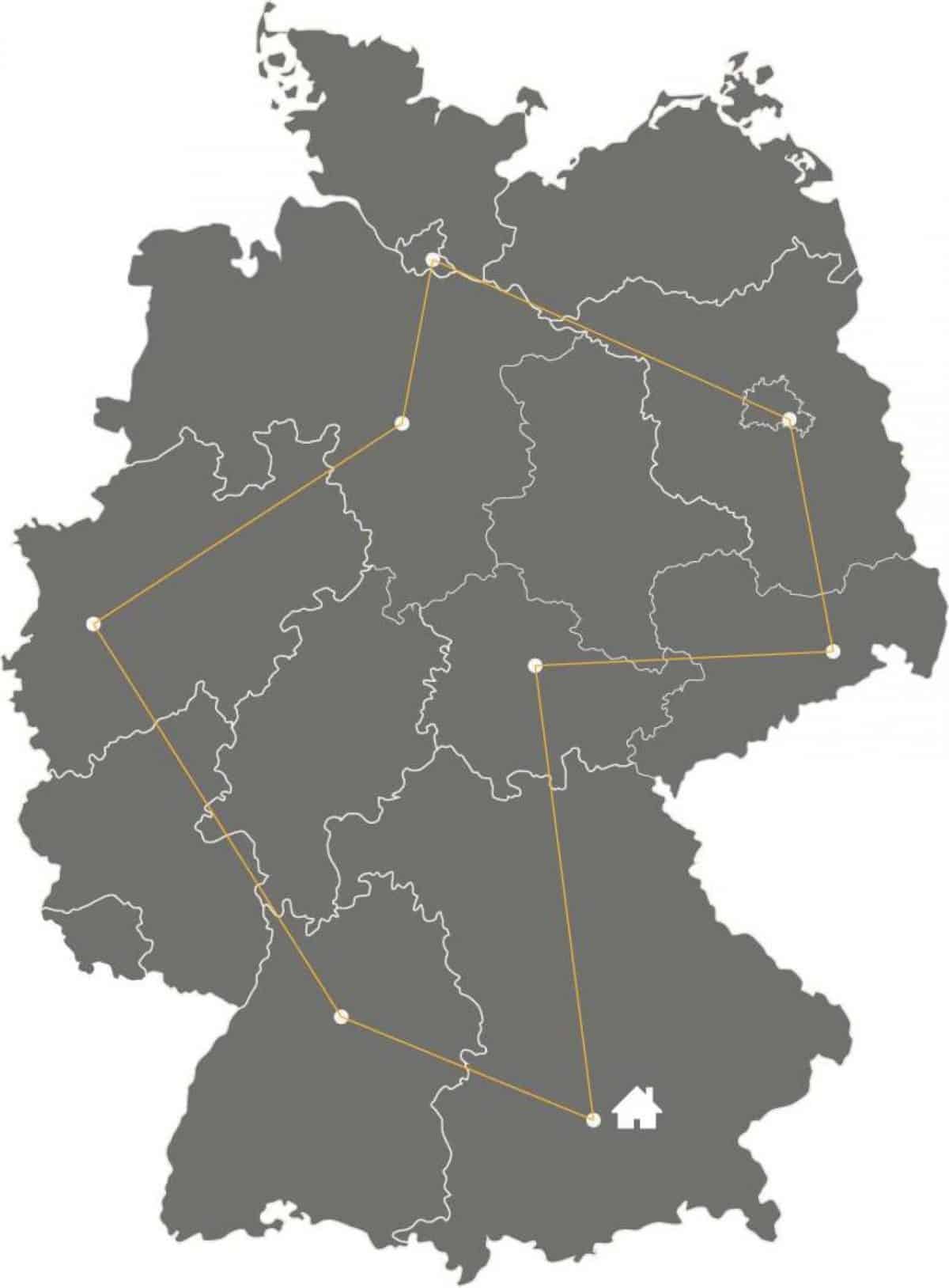Die optimale Tour für den Techniker ist um etwa 17% kürzer als der erste Vorschlag.

In Summe ergibt sich eine Effizienzsteigerung von 17% durch die optimale Route.

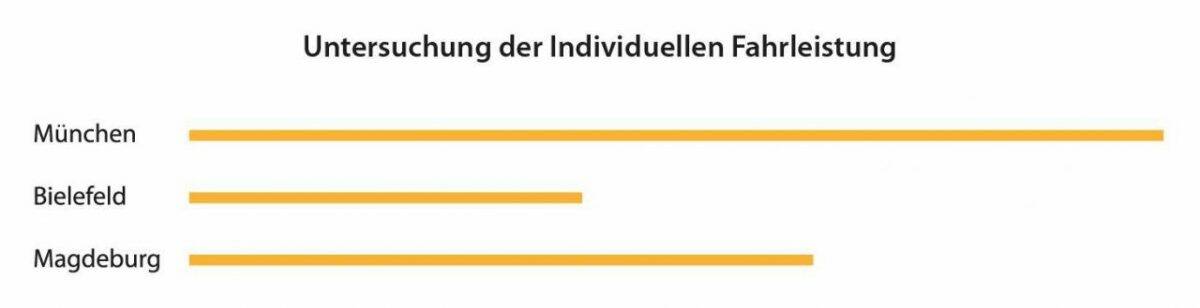
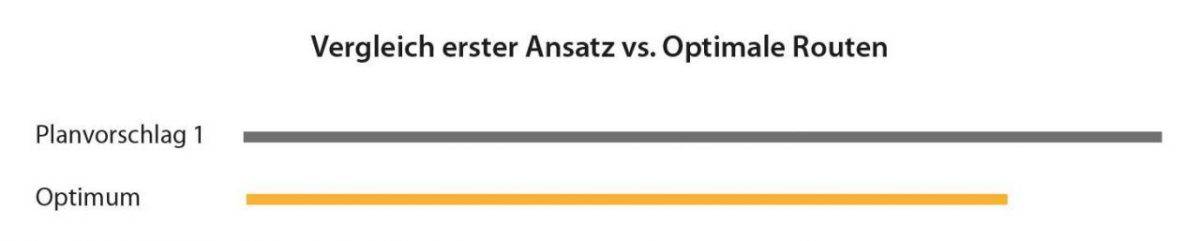Vergleich der Fahrleistung zwischen dem ersten Planvorschlag und der optimalen Route.

Mehr Servicetechniker – mehr Optionen

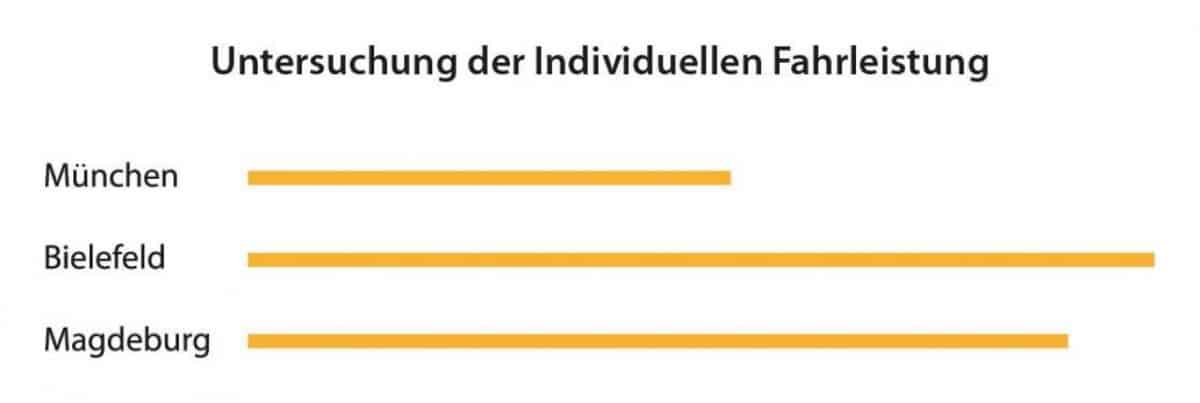
Fügen wir dem Ausgangsproblem nun zwei weitere Kollegen in Magdeburg und Bielefeld hinzu, steigt die Anzahl der möglichen Kombinationen um ein Vielfaches. Mathematisch ist dieses Problem als „Tourenplanungs-Problem mit mehreren Standorten und fixierten Zeitfenstern“ bekannt, bzw. auf Englisch Multi-Depot Vehicle Routing Problem with Time Windows, abgekürzt MDVRPTW.

In der Erweiterung des Problems werden zusätzliche Techniker in Bielefeld und Magedeburg ergänzt.

Löst man das Problem analog zum ersten Vorgehen – Reise zum nächstgelegenen Zielort, der noch nicht besucht wurde, ergibt sich spätestens nach dem zweiten Einsatz die Frage, welcher der drei Techniker drei Aufträge übernehmen muss, während seine Kollegen nur zwei Vorgänge zu erledigen haben. Wir gehen an dieser Stelle der Einfachheit halber davon aus, dass alle Aufträge gleich lang dauern und inklusive Fahrtstrecke an einem Arbeitstag erledigt werden können.

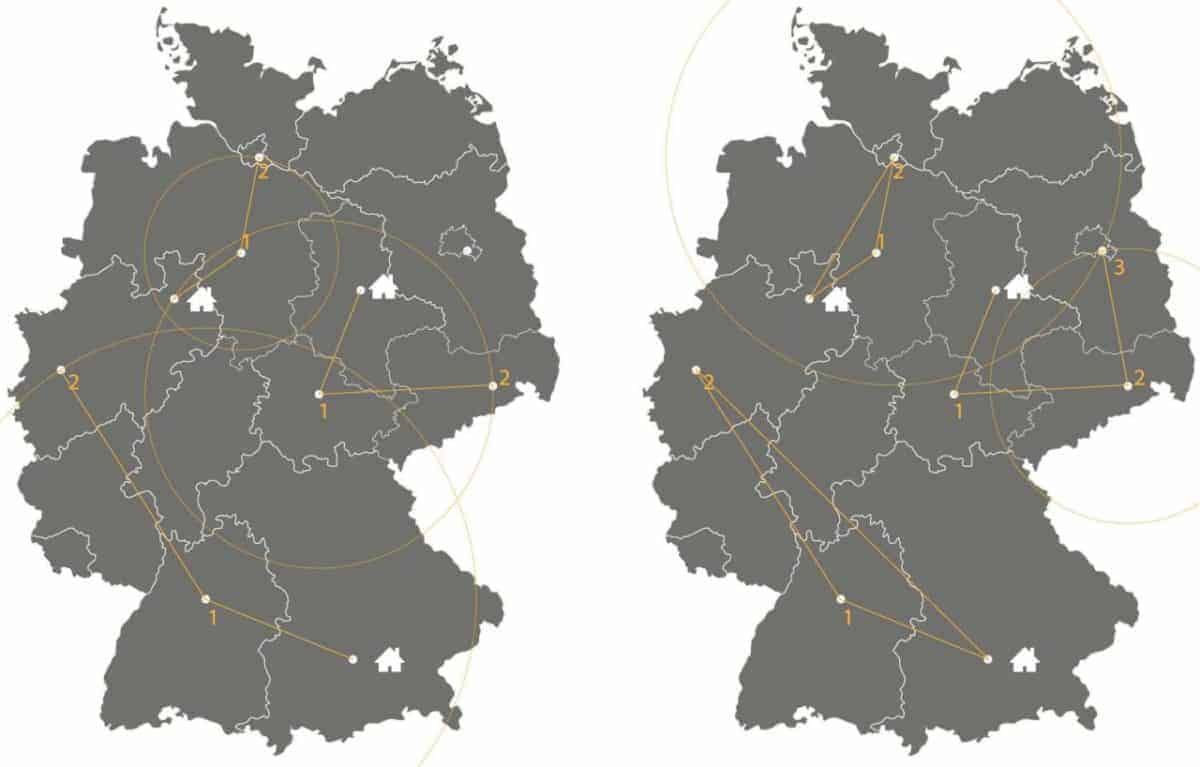Durch diese Erweiterung wird die Aufgabenstellung komplexer. Wir nähern uns wieder mit dem gleichen Ansatz wie zuvor.

Wer muss mehr arbeiten?

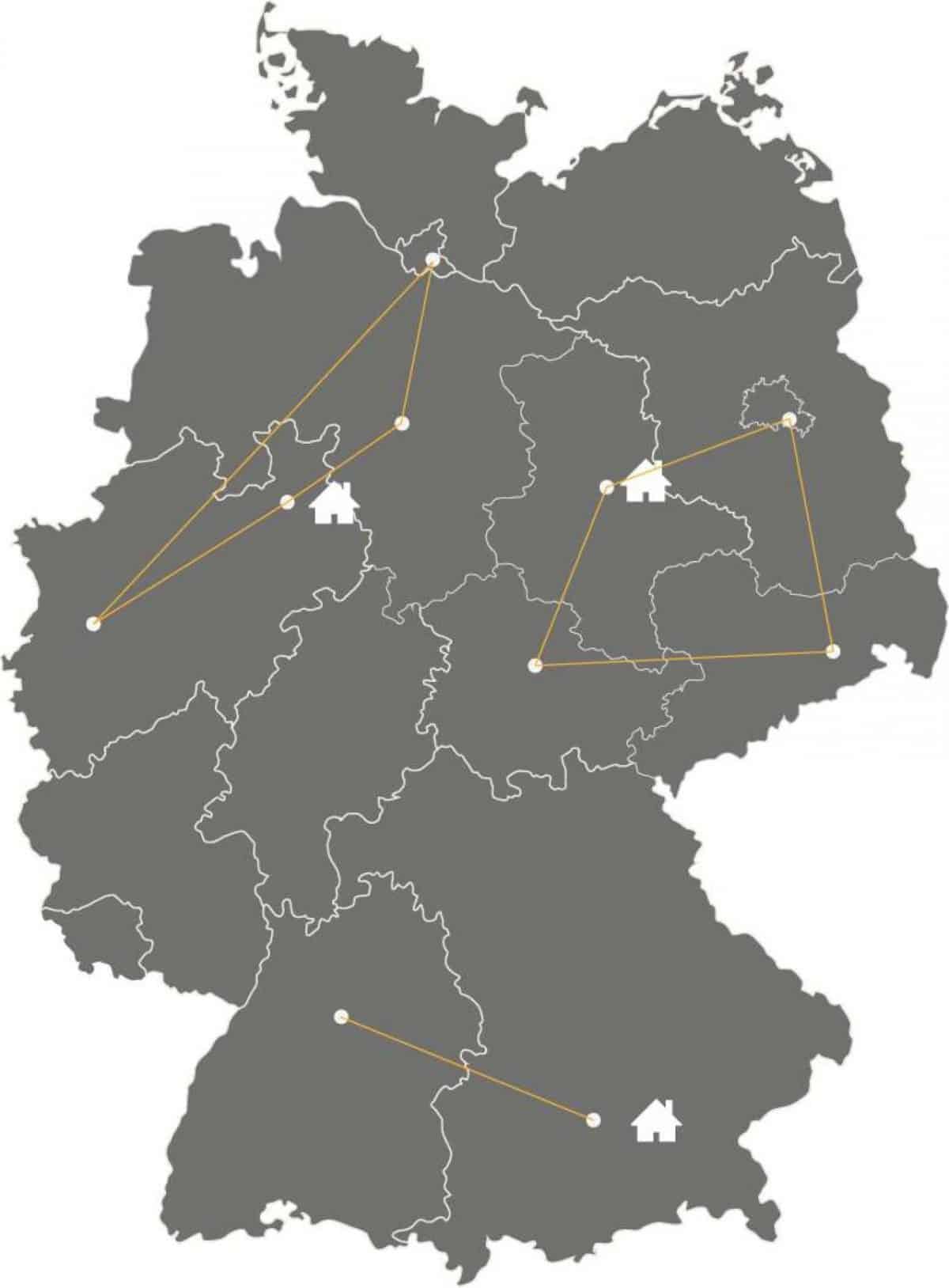
Die Entscheidung, wer den dritten Auftrag übernehmen muss, wird in diesem Szenario zwischen den Monteuren aus Bielefeld und Magdeburg getroffen, wenn sie jeweils bei ihrem zweiten Auftrag in Erfurt bzw. Hamburg sind. Da die Fahrtstrecke von Erfurt nach Berlin kürzer ist, als von Hamburg nach Berlin, muss der Kollege aus Magdeburg den Auftrag übernehmen.

Nach diesem Ansatz muss einer der Mitarbeiter muss vier Aufträge übernehmen.

Daraus ergeben sich drei in sich abgeschlossene Routen ohne Überschneidungen. Die Lastenverteilung ist relativ gerecht, auch wenn der Münchener Techniker mehr als doppelt so viel fahren muss wie sein Kollege aus Bielefeld:

Eine gerechte Lastenverteilung ist in dieser Konstellation kaum zu erreichen.

Sieht optisch gut aus, aber ist das auch optimal?

In Punkto Gesamtfahrleistung ist dieser Planungsvorschlag allerdings wieder nicht optimal, vor allem, weil der Münchener Techniker die weite Strecke von Stuttgart nach Düsseldorf fahren muss.

Der optimale Planvorschlag für dieses Szenario.

Eine deutlich kürzere Gesamtstrecke ist möglich, wenn der Münchener Techniker nur den Auftrag in Stuttgart erledigt und danach wieder zurückkehrt.

Dieser Planvorschlag ist in Bezug auf die Wirtschaftlichkeit (gemessen an der Fahrtstrecke) um etwa 15% effizienter als der erste Planvorschlag.

Der Planvorschlag ist um ca. 15% effizienter.

Allerdings führt dieser Planvorschlag zu einer noch deutlicheren Ungleichverteilung unter den Ressourcen: So fährt der Münchener Techniker nur die Hälfte der Wegstrecke seiner beiden nördlichen Kollegen.

Nach wie vor ist die Arbeitslast nicht gerecht verteilt.

Dieses theoretische Szenario zeigt grundsätzlich die Komplexität der Herausforderung „optimale Tourenplanung“ auf. Allein schon bei nur acht Aufträgen und drei Technikern ergeben sich Millionen Kombinationsmöglichkeiten, die kein Mensch im Kopf berechnen kann.

In der Praxis wird die Planung durch viele andere Kriterien zusätzlich erschwert: Hier gibt viele weitere Aspekte, die bei der Planung zu berücksichtigen sind, wie z.B. zeitlich fixierte Aufträge (Aufträge, die zu einem fest definierten Zeitpunkt erledigt werden müssen), festgelegte Reaktionszeiten (spätestens 2 Stunden nach Ausfall muss ein Techniker vor Ort sein), Abhängigkeiten (z.B. erst muss Material geliefert werden, dann kann der Techniker zum Einsatz fahren), Skills (nicht jeder Techniker kann alles) und vieles mehr.

Diese Einschränkungen reduzieren zwar die Anzahl der möglichen Reihenfolgen erheblich, gleichzeitig erschweren die zusätzlichen Kriterien die Berechnung der „optimalen“ Tour für einen Menschen.

Unser Beispiel ist stark vereinfacht – in der Praxis kommen viele andere Kriterien hinzu, die die Planung weiter einschränken.

Eine Software zur Einsatzplanung, wie SAP MRS oder alternative Lösungen, unterstützt den Disponenten bei der Einsatzplanung. Eine Software kann in Sekunden Millionen von Tourenkombinationen miteinander vergleichen und so mit hoher Treffsicherheit eine möglichst ideale Route finden.

Mehr zur Herausforderung, die optimale Tour zu planen finden Sie in unserem Ratgeber Tourenplanung im Außendienst.